killopat.blogg.se - Four parameter logistic regression with polymath software

FOUR PARAMETER LOGISTIC REGRESSION WITH POLYMATH SOFTWARE HOW TO

For asymmetric logistic curves, a five parameter logistic (5PL) curve is required.įor technical assistance on using this calculator, please contact tool has recently been updated. Note that four parameter logistic (4PL) curves are symmetric in nature around the inflection point.

Hill coefficient: the slope of the curve at the inflection point.

Inflection point: the dose at which the curvature of the response line changes where the rate of change switches signs often referred to as the IC50 or EC50.

Maximum: the point of greatest response.

Minimum: the point of smallest response can be baseline response, control or response when treatment concentration is zero.

Beyond this linear range, the responses quickly plateau and approach the minimum and maximum.įour parameter logistic curve refers to the following four parameters: This type of curve is particularly useful for characterizing bioassays because bioassays are often only linear across a specific range of concentration magnitudes. They follow a sigmoidal, or "s", shaped curve. You could also use log(conc+1) in your formula as well, as concentration can never go negative.Four parameter logistic (4PL) curve is a regression model often used to analyze bioassays such as ELISA. If your data are discrete counts as opposed to some continuous measure you could also use family=poisson with a log link, or work with a log(y+1) transformed dependent variable. a model of the form require(scam)įit = scam(y~s(conc,k=nknots,bs="mpi",m=2), family=gaussian, data=data) Myself I had more luck using a constrained strictly monotone P spline fit though, fitted using the scam package, to do calibration curves, as that resulted in much narrower 95% confidence intervals and prediction intervals than using the four parameter logistic model. See the manuscript: The Five Parameter Logistic: A Characterization And Comparison With The Four Parameter Logistic for more information on STATLIA MATRIX’s 5PL curves.

FOUR PARAMETER LOGISTIC REGRESSION WITH POLYMATH SOFTWARE HOW TO

And it also covers how to do inverse prediction and calculating derived statistics like determining the limit of detection, limit of quantification and working range. STATLIA MATRIX uses powerful numeric algorithms plus accurate weighting with the test’s historical data to provide the gold standard for 5PL curve fitting in analysis software. They also show how one could use weights and iteratively refitted least squares to allow for non-homogeneous variance. Geom_point(data=ame(x=x,y=y), aes(x=x, y=y, ymin=NULL, ymax=NULL), size=5, col="blue") + Geom_line(data=confintervals, aes(x=x, y=fit), colour=I("blue"), lwd=2) + Geom_ribbon(data=confintervals, aes(x=x, ymin=lwr, ymax=upr), fill=I("blue"), alpha=I(0.2)) + Qplot(data=predintervals, x=x, y=fit, ymin=lwr, ymax=upr, geom="ribbon", fill=I("red"), alpha=I(0.2)) + Predintervals = ame(x=xvals,predFit(nlslmfit, newdata=ame(x=xvals), interval="prediction"))Ĭonfintervals = ame(x=xvals,predFit(nlslmfit, newdata=ame(x=xvals), interval="confidence")) They just use the nlsLM function in the minpack.lm package.

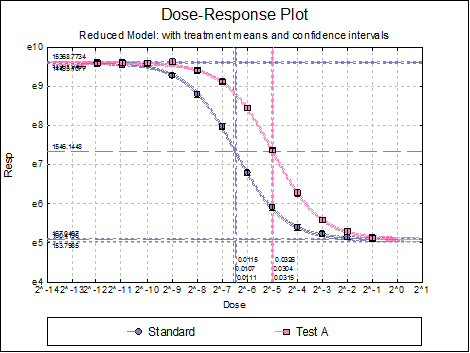
There is an excellent R tutorial on fitting the 4 parameter logistic model for calibration purposes (e.g. Response<-0.5 #lets use 0.5 for the responseĭOSEx<-ED(model1,response,type="absolute",display=F) # the estimated DOSE # type="absolute" gives you the ability to use absolute values for the response, to

# the index (display=F is a good option also) # The result is a matrix, from which the Estimate values can be extracted using # the ED function is used to give the EDx value. If you want to estimate the DOSE from SLOPE, or 'Concentration' from 'OD' in case of an ELISA, just use the ED function of the 'drc' package 'predict' is not the best way to estimate the DOSE from SLOPE in this case, because you have to reverse them in your model2, which doesn't work in this example. "Upper", "ED50")),data=spinach) predict(model2, newdata, Model2 <- drm(DOSE~SLOPE, CURVE, fct=LL.4(names=c("Slope", "Lower", Library(drc) model1 <- drm(SLOPE~DOSE, CURVE,įct=LL.4(names=c("Slope", "Lower", "Upper", "ED50")),data=spinach)